[日本語まとめ] VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation
Jiyang Gao, Chen Sun, Hang Zhao, Yi Shen, Dragomir Anguelov, Congcong Li, Cordelia Schmid
- Arxiv
- Blog “Predicting behavior to help the Waymo Driver make better decisions”
- YouTube
- VectorNet: Encoding HD Maps and Agent Dynamics from Vectorized Representation [Paper Explained]
どんなもの?
道路上では車がレーンチェンジして、自動運転車両が走行している前のスペースに入ってきたり、目の前に走っている自転車が突然曲がり、目の前を横切るようなシーンで溢れている。車や自転車、人などの道路の利用者の意図を理解することが、安全な運転を行うために必要である。しかしながら道路の利用者の行動を予測することは難しい。精度の高い予測を行うためには道路の幅や形状、信号、標識など様々な道路の情報、交通ルールを理解する必要がある。さらに他の車や人はいつも交通ルールを守るとは限らないことも考える必要がある。
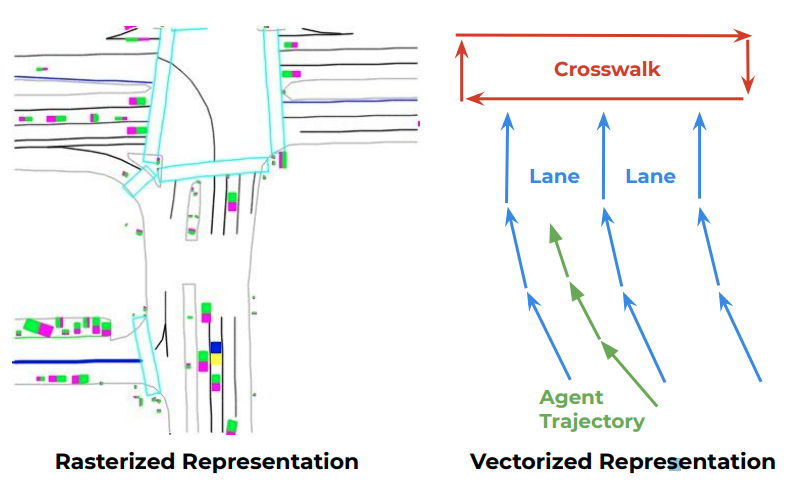
この論文は車や人などの道路上の利用者の行動を経路として予測するVectorNetを提案する。VecotrNetは利用者の過去の経路や道路情報をpolylineで表現する。Polylineは始点と終点、その属性を持つベクトルの集まりである。
VectorNetは階層的なグラフニューラルネットワークである。各polylineをノードと見なし、構成したサブグラフからpolylineの局所的な特徴量を計算するPolyline subgraphs network、polyline間の大域的な関係を計算するGlobal Interaction Graph、マスクされたpolylineを補間するSupervision、Global Interaction Graphで計算した特徴量からターゲットの予測経路をデコードするPredictionで構成される。
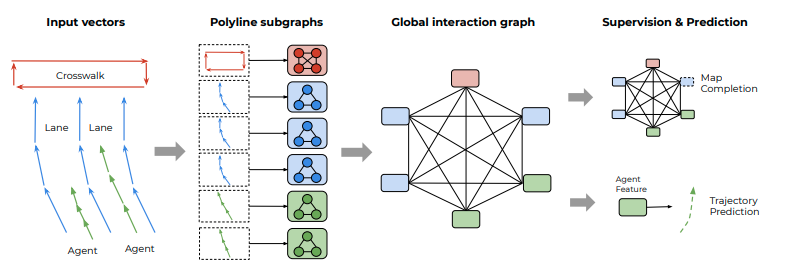
またVectorNetの提案に加えて、本論文では不完全なグラフを補完する補助タスク(auxiliary graph completion task)を提案する。グラフ補完タスクは以下の成功を得た論文に習った補助タスクであり、訓練時に将来の経路を予測するタスクに加えて使用する。
-
BERT: Pre-training of deep bidirectional transformers for language understanding(arxiv)
-
VideoBERT: A joint model for video and language representation learning(arxiv)
グラフ補完タスクはGlobal Interaction Graphのノードをランダムにマスクする。そしてその他のノードからマスクしたノードを再構成する。不完全なグラフを補完することで、VectorNetが道路の利用者のダイナミクスや道路構造物の相互作用を捉えるのを促進させる。
先行研究と比べてどこがすごい?何を解決したか?
ラスタライズアプローチは車の頭上から地面を見下ろした俯瞰図として道路情報を表現し、CNNで処理する方法である。ラスタライズアプローチの欠点は計算量が多く、その描画および処理に時間を必要とすることである。構造物を正しく描画するためには大きな俯瞰図を必要とするが、そうなると描画した俯瞰図に道路構造物がない空のピクセルが多く存在することになる。VectorNetで用いるpolyline表現およびグラフ処理はレンダリングによる無駄なスペースがないため、計算量を削減できる。具体的にはVectorNetは従来の方法であるラスタライズアプローチと比較して、70%のモデルサイズおよびFLOPSが桁レベルで小さい場合でも同等もしくは最も良い予測性能を達成する。
手法は?
VectorNetのパイプラインは次のとおりである。
- 各道路の利用者および各道路構造物を一つのpolylineで表現する
- 各polylineに対してPolyline Subgraphs Networkを使い、polylineの局所的な特徴量を計算する
- polylineの局所的な特徴量をノードとしてGlobal Interaction Graphを使いpolyline間の大域的な特徴量を計算する
- 経路を予測するターゲットのpolyline特徴量から経路をデコードする
- 訓練時のみ、Global Interaction Graphのノードをマスクし、マスクされていないノードからマスクされたノードを推定する
Polyline表現
各道路の利用者および各道路構造物を一つのpolylineで表現する。Polyline \(\mathcal{P}\)はベクトル\(\{ \mathbf{v}_1, \mathbf{v}_2, \dots \}\)で構成される。Polylineに含まれるベクトル\(\mathbf{v}_i\)は次の情報を持つ。
\[\mathbf{v}_i = [\mathbf{d}_i^s, \mathbf{d}_i^e, \mathbf{a}_i, j ]\]- \(\mathbf{d}_i^s\)および\(\mathbf{d}_i^e\)は2次元または3次元のベクトルの始点と終点である。これらの点がグローバル座標系で表されると、点の位置に応じてネットワークの出力が変化し、精度に影響する。位置に対するネットワークの出力を不変にするために、最後に観測された予測ターゲットの場所を中心とする座標系で表現する。
- \(\mathbf{a}_i\)は物体の種類(車、人などの利用車または道路構造物)や経路のタイムスタンプ、道路の制限速度である。
- \(j\)は\(\mathbf{v}_i\)が含まれているpolyline \(\mathcal{P}_j\)のIDである。
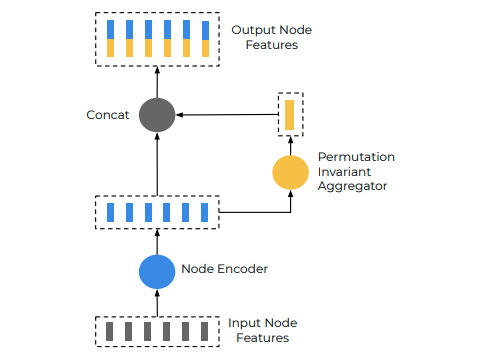
Polyline Subgraphs Network
Polyline Subgraphs Networkはpolylineの特徴量を計算する。各pollylineごとに次の計算を行う。
-
サブグラフの構成
Polyline \(\mathcal{P}\)に属する各ベクトル\(\{ \mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_P \}\)をノードしてサブグラフ\(\{ \mathbf{v}_1^{(0)}, \mathbf{v}_2^{(0)}, \dots, \mathbf{v}_P^{(0)} \}\)を構成する。
-
サブグラフの伝播
次の伝播操作を繰り返し、\(l\)層のノードの特徴量から\(l+1\)層のノードの特徴量を計算する。
\[\mathbf{v}_i^{(l+1)} = \psi_{\text{rel}} \left( g_{\text{enc}}(\mathbf{v}_i^{(l)}), \psi_{\text{agg}} \left( \{ g_{\text{enc}}(\mathbf{v}_j^{(l)}) \} \right) \right)\]\(g_{\text{enc}}\)は入力されたノード特徴量をエンコードする関数、\(\psi_{\text{agg}}\)は\(\mathbf{v}_i^{(l)}\)の周辺のノードを集約する関数、\(\psi_{\text{rel}}\)は\(\mathbf{v}_i^{(l)}\)とその周辺ノード\(\{ \mathbf{v}_j^{(l)} \}\)の関係演算子である。\(g_{\text{enc}}\)はfully connected layer, layer normalization, ReLUからなるMLP、\(\psi_{\text{agg}}\)はmaxpooling、\(\psi_{\text{rel}}\)はconcatenationを使って実現する。
-
polyline \(\mathcal{P}_j\)の特徴量を計算する。
\[\mathbf{p} = \psi_{\text{agg}} \left( \{ \mathbf{v}_i^{(L_p)} \} \right)\]
polylineに含まれるベクトルの開始地点と最終地点を同じに点にして、特徴量を\(\mathbf{a} = 1\)としたとき、PointNetと同様にアーキテクチャになることから、Polyline Subgraphs NetworkはPoinNet(arxiv)の一般系とみなすことができる。ただし道路の利用者の経路や道路構造物の成り立ちからpolyline表現への埋め込みやサブグラフのノード接続を行っている。この制限によって経路や構造物をエンコードするのに特化した構造である。
Global Interaction Graph
Global Interaction Graphはpolylineの特徴量をノードとして、グラフニューラルネットワークにより次の伝播操作を繰り返して大域的な特徴量を計算する。
\[\{ \mathbf{p}_i^{(l+1)} \} = \text{GNN} \left( \{ \mathbf{p}_i^{(l)} \}, \mathcal{A} \right)\]\(\{ \mathbf{p}_i^{(l)} \}\)は\(l\)層のノード特徴量のセットである。\(\mathcal{A}\)はノード同士の接続を示す隣接行列である。隣接行列\(\mathcal{A}\)は設定可能な行列である。例えば”Social LSTM: Human Trajectory Prediction in Crowded Space”では空間上の距離をつかったheuristicにより隣接行列を計算している。VectorNetでは簡単のため全結合グラフを使う。GNNはself-attentionを使って実装する。
\[\text{GNN}(\mathbf{P}) = \text{softmax} (\mathbf{P}_Q \mathbf{P}_K^{T}) \mathbf{P}_V\]\(\mathbf{P}\)はノード特徴行列であり、\(\mathbf{P}_Q, \mathbf{P}_K, \mathbf{P}_V\)は線形投影である。実験ではGlobal Interaction Graphの伝播操作の回数\(L_t\)を1回とした。
将来の経路のデコード
Global Interaction Graphにより計算された特徴量\(\{ \mathbf{p}_i^{(L_t)} \}\)の内、ターゲットの道路の利用者のpolyline特徴量\(\mathbf{p}_i^{(L_t)}\)から将来の経路\(\mathbf{v}_i^{\text{future}}\)をデコードする。
\[\mathbf{v}_i^{\text{future}} = \psi_{\text{traj}} \left( \mathbf{p}_i^{(L_t)} \right)\]\(\psi_{\text{traj}}\)は経路のデコーダである。デコーダとしてMLPを使う。
Auxiliary graph completion task
マスクされていないpolyline特徴量からマスクされたpolyline特徴量を推定するデコーダ\(\psi_{\text{node}}\)を訓練時に追加する。
\[\hat{\mathbf{p}}_i = \psi_{\text{node}}(\mathbf{p}_i^{(L_t)})\]ただし、\(\psi_{\text{node}}\)はMLPである。Global Interaction Graphはpolylineの特徴量をノードに持つ全結合で順序がないグラフである。あるpolylineの特徴量がマスクされているとき、個々のpolylineノードを識別する必要がある。そこで識別子の埋め込み(Identifier embedding) \(\hat{\mathbf{p}}_i^{id}\)をGlobal Interaction Graphの入力ノードに加える。
\[\mathbf{p}_i^{(0)} = [\mathbf{p}_i ; \mathbf{p}_i^{id} ]\]識別子の埋め込み\(\hat{\mathbf{p}}_i^{id}\)は特徴量\(\mathbf{p}_i\)に対応するpolylineを構成するすべてのベクトルの開始地点\(\mathbf{d}_i^s\)の最小値である。
目的関数
次のマルチタスク目的関数を使ってVectorNetを訓練する。
\[\mathcal{L} = \mathcal{L}_{\text{traj}} + \alpha \mathcal{L}_{\text{node}}\]\(\mathcal{L}_{\text{traj}}\)は真の経路に対する負のガウシアン対数尤度、\(\mathcal{L}_{\text{node}}\)はマスクされた特徴量と推定した特徴量とのHuber損失、\(\alpha\)は2つの損失のバランスを取るための係数である。ただしネットワークは特徴量の大きさを小さくすることで損失\(\mathcal{L}_{\text{node}}\)を低くすることができる。この特徴量の大きさによるグリッチを回避するため、Global Interaction Graphに入力する前に特徴量を正規化する。
どうやって有効だと検証した?
Ablation Study
まだ
計算コスト
性能検証
課題は?議論はある?
複数経路予測のためのPolyline表現
Polyline表現においてターゲットの利用者の位置に対してネットワークの出力を不変にするために、polylineに属するすべてのベクトルを最後に観測されたターゲットの場所を中心とする座標系で正規化した。一つのターゲットだけでなく相互作用するすべてのエージェントの予測を並列に行うためには、すべてのエージェントの座標中心を共有することが考えられる。
多様な経路を出力するVectorNetの経路デコーダ
提案したVectornetは一つの経路を出力する。より多様な経路を出力するため、以下の論文で提案されたデコーダをMLPの代わりに使うことが考えられる。
- Multipath: Multiple probabilistic anchor trajectory hypotheses for behavior prediction(arxiv)
- Multiple futures prediction(arxiv)
次に読むべき論文は?
Multimodal Motion Prediction with Stacked Transformers
SPAGNN: Spatially-Aware Graph Neural Networks for Relational Behavior Forecasting from Sensor Data
SCENE TRANSFORMER: A UNIFIED ARCHITECTURE FOR PREDICTING MULTIPLE AGENT TRAJECTORIES
個人的メモ
なし