[日本語まとめ] PRECOG: PREdiction Conditioned On Goals in Visual Multi-Agent Settings
Nicholas Rhinehart, Rowan McAllister, Kris Kitani, Sergey Levine
どんなもの?
自動運転車が人間とともに道路上で動作するためには、他のドライバーの行動を予測することが必要である。特に自動運転の条件判断や経路計画に必要とされる予測はただ漠然とした単純な予測ではない。自動運転車両が目的を達成する意図に応じて他のエージェントが何をする可能性が高いかを示す予測が必要とされる。
この論文は条件判断のために複数の車(マルチエージェント)の行動を予測する方法ESPおよびESPを使用した条件付き予測方法PRECOGを提案する。ESPおよびPRECOGは自動運転車両も含めたマルチエージェントの相互作用を考慮した予測を行う。予測した行動は2次元位置で構成される経路として出力される。

ESP(Estimating Social-forecast Probabilities)は単一エージェントの経路を予測するR2P2(link, summary)をベースとした自己回帰型フローベースの生成モデルである。ESPはマルチエージェント間の相互作用を捉えるように、各エージェントおよび各タイムステップで分散表現された潜在変数とすべてのエージェントの一時刻前の状態を利用して次の時刻の状態を計算する。そしてこの計算を予測時刻まで繰り返すことで将来の経路を生成する。あるエージェントおよびある時刻の特定の潜在変数を変更することで、その変更による影響を加味した予測を行うことができる。また各予測の尤度を計算することもできる。
PRECOG (PREdition Conditioned On Goal)は自動運転車両の目的地を条件としてエージェントの将来の経路を予測する方法である。PRECOGはESPを使用して自動運転者がゴールに向かうような経路を潜在変数で求めた後、その潜在変数を利用して再度ESPを使用することで条件付き予測を行う。自動運転車が目的地へ向かう場合に集中して予測するので、予測する経路の可能性を絞ることができる。
先行研究と比べてどこがすごい?何を解決したか?
- ESPがエージェント間の相互作用を考慮する予測を実行できることを示した。
- ESPがCALRAおよびnuScenesのデータセットで現状の3つのstate-of-artの方法の性能を上回ることを示した。
- PRECOGが自動運転車両だけでなく相互に作用するその他のエージェントの予測性能が改善されることをCALRAおよびnuScenesのデータセットを使い示した。
手法は?
Estimating Social-forecast Probability (ESP)
ESPはマルチエージェントの将来の経路の分布\(q(\mathbf{S} \mid \phi; \mathcal{D})\)を表す状態の遷移確率を正規分布と仮定した自己回帰型のフローベースの生成モデルである。
\[q(\mathbf{S}_t \mid \mathbf{S}_{1:t-1}, \phi) = \overset{A}{\underset{a=1}{\prod}}\mathcal{N}(\mathbf{S}_t^a ; \mu_{\theta}^a, \sigma_{\theta}^a{\sigma_{\theta}^a}^{\top})\]パラメータ\(\mu_{\theta}^a(\cdot) \in \mathbb{R}^{D}\)および\(\sigma_{\theta}^a(\cdot)\in \mathbb{R}^{D \times D}\)は時刻\(t\)におけるエージェント\(a\)の状態\(\mathbf{S}_{t}^a\)の平均および標準偏差を出力するネットワーク関数である。これのアーキテクチャは次のセクションで説明する。
ESPの潜在変数は各エージェントの各タイムステップに分解されて表現される。
\[\mathbf{Z} = \mathbf{Z}_{1:T}^{1:A} = \{\mathbf{Z}_1^1, \dots, \mathbf{Z}_T^1, \mathbf{Z}_1^2, \dots, \mathbf{Z}_T^2, \dots, \mathbf{Z}_1^{A}, \dots, \mathbf{Z}_T^{A}\}, \mathbf{Z}_t^a \sim \mathcal{N}(0, I)\]ESPこの潜在変数\(\mathbf{Z}\)をもとにA個のエージェントの時刻Tまでの経路\(\mathbf{S}\)を生成する。具体的には次に示す1ステップ先の更新式をすべてのエージェントで現在時刻から繰り返し適用する。
\[\mathbf{S}_{t}^{a} = f_{\theta}(\mathbf{Z}_t^a) = \mu_{\theta}^a(\mathbf{S}_{1:t-1}, \phi) + \sigma_{\theta}^a(\mathbf{S}_{1:t-1}, \phi) \cdot \mathbf{Z}_t^a \in \mathbb{R}^{D}\]また経路から潜在変数の変換、経路の尤度の計算は次の式を使う。
\[\mathbf{Z}_t^a ={\sigma_{\theta}^a}^{-1}(\mathbf{S}_{1:t-1}, \phi) \left( \mathbf{S}_{t}^{a} - \mu_{\theta}^a(\mathbf{S}_{1:t-1}, \phi) \right)\] \[q(\mathbf{S} \mid \phi; \mathcal{D})= \mathcal{N}(f_{\theta}^{-1}(\mathbf{S} ; \phi;0, I)) \big| \det \frac{\mathbf{d}f_{\theta}}{\mathbf{d} \mathbf{Z}}_{\mathbf{Z} = f_{\theta}^{-1}(\mathbf{S}; \phi)} \big|\]アーキテクチャー
ESPのネットワークアーキテクチャを次の図に示す。
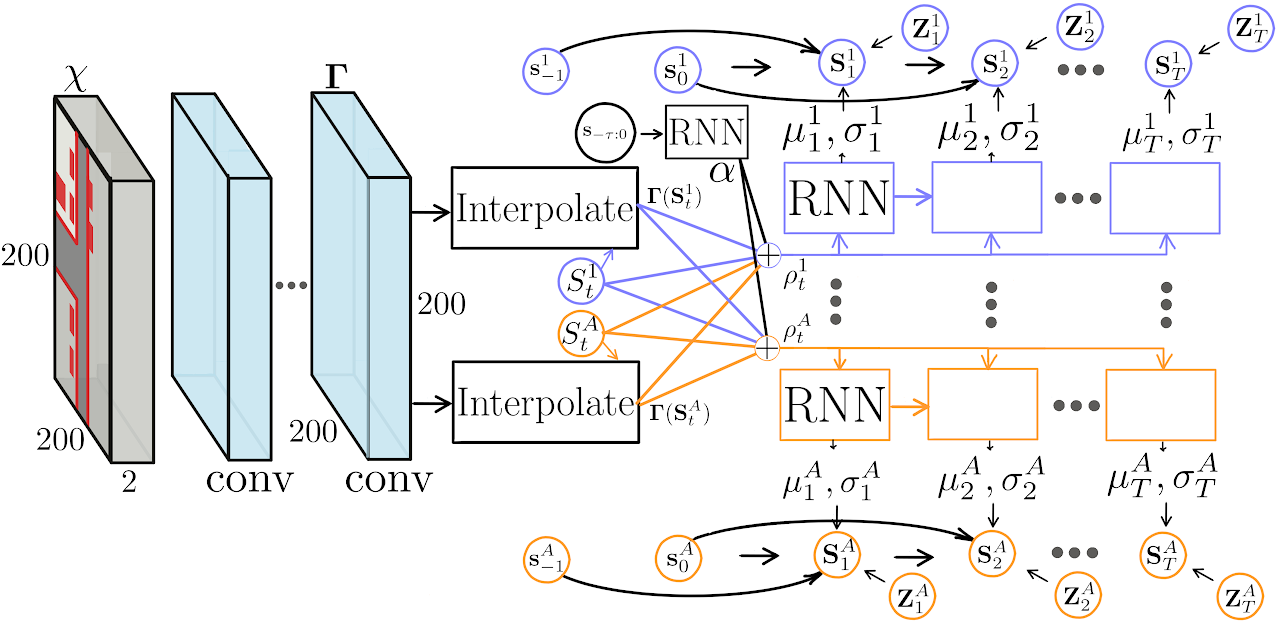
図で示すようにESPは観測マップ\(\chi\)から特徴マップ\(\Gamma\)を計算するCNN、各エージェントの過去の経路の特徴を計算するRNN、そして将来の経路を計算するRNNで構成される。このネットワークは次の手順で動作する。
-
現在時刻で得られたLIDARの点群と道路をラスタライズしてテンソルを作り、CNNで処理して特徴マップ\(\Gamma\)を計算する
-
過去から現在までのすべてエージェントの位置をエージェントごとにRNN(GRU)を使って特徴量\(\alpha\)を計算する
-
時刻\(1:T\)までの以下のステップを繰り返す
-
時刻\(t\)の各エージェントの位置\(\mathbf{s}_{t-1}^a\)に対応した空間特徴量\(\Gamma(\mathbf{s}_{t-1}^a)\)をbilinear補間により特徴マップ\(\Gamma\)から取り出す
\[\Gamma^{1:A} = \{ \Gamma(\mathbf{s}_{t-1}^1),..., \Gamma(\mathbf{s}_{t-1}^A) \}\] -
各特徴量\(\alpha\)、\(\mathbf{s}_{t}^{1:A}\)、\(\Gamma^{1:A}\)をConcatenationして特徴\(p_{t-1}\)を作成する
-
特徴\(p_{t-1}\)から予測用のRNN(GRU)を使い、ベレの方法(wiki)のステップ\(m_{\theta}\)と位置の標準偏差\(\sigma_{\theta}\)を計算する
-
ベレの方法を使って位置の平均を求める
\[\mu = 2 \mathbf{s}_{t-1}^a - \mathbf{s}_{t-2}^a + m_{\theta}\] -
Reparametrization Trickを使い状態\(\mathbf{s}_{t}^a\)を計算する
\[\mathbf{s}_{t}^a = \mu_{\theta} + \sigma_{\theta} \cdot \mathbf{z}_t^a\]
-
ESPの学習
ESPは訓練データ\(\mathcal{D}\)を使って対数尤度を最大化するように訓練される。
\[\max_{\theta} \mathbb{E}_{(s, \phi) \sim \mathcal{D}} \log q(\mathbf{S} \mid \phi)\]PREdiction Conditioned On Goals (PRECOG)
ESPを使った条件付き運動予測を行うPRECOGのアルゴリズムは次の通りである。
-
Imitative planning(arxiv, summary)により自動運転車両がゴールに止まるような潜在変数\(\mathbf{z}_{1:T}^0\)を求める
-
自動運転車両の潜在変数\(\mathbf{z}_{1:T}^0\)を正規分布からサンプルする
-
自動運転車両の潜在変数が収束するまで以下を繰り返す
-
その他のエージェントの潜在変数\(^{1:K}\mathbf{z}\)を正規分布から\(K\)回サンプリングする
\[^{1:K}\mathbf{z}_{1:T}^{1:A-1} \overset{iid}{\sim} \mathcal{N}(0, I)\] -
マルチエージェントの模倣尤度とゴールの尤度の和の期待値\(\mathcal{L}(\mathbf{z}^r, \mathcal{G})\)を計算する。
\[\mathcal{L}(\mathbf{z}^0, \mathcal{G}, \phi) = \mathbb{E}_{\mathbf{Z}^{1:A}} \left[ \log q(f(\mathbf{Z}) \mid \phi) + \log q(\mathcal{G} \mid f(\mathbf{Z}), \phi) \right]\]\(\log q(f(\mathbf{Z}) \mid \phi)\)は訓練データで学習した経路とどれだけ近いかを示す尤度、\(q(\mathcal{G} \mid f(\mathbf{Z}), \phi)\)は自動運転車両からゴールに向かうまでのウェイポイント\(\mathbf{w}\)を使ったゴールの尤度である。
実際には前ステップでサンプリングした潜在変数を使って期待値の近似値を計算する。
\[\hat{\mathcal{L}}(^{1:K}\mathbf{z}, \mathcal{G}, \phi) = \frac{1}{K} \sum_{k=1}^{K} \log( p(f(^k\mathbf{z}) \mid \phi) p(\mathcal{G} \mid f(^k\mathbf{z}), \phi) )\] -
期待値を最大化するようにGradient Ascentによって自動運転車の潜在変数を更新する。
\[\mathbf{z}_{1:T}^0 \leftarrow \mathbf{z}_{1:T}^0 + \Delta_{\mathbf{z}_{1:T}^0} \hat{\mathcal{L}}(^{1:K}\mathbf{z}, \mathcal{G}, \phi)\]
-
-
-
その他のエージェントの潜在変数\(^{1:K}\mathbf{z}\)を正規分布から\(K\)回サンプリングする
\[^{1:K}\mathbf{z}_{1:T}^{1:A-1} \overset{iid}{\sim} \mathcal{N}(0, I)\] -
自動運転車両とその他のエージェントの潜在変数を連結する
\[^{1:K}\mathbf{z}_{1:T}^{1:A} = [\mathbf{z}_{1:T}^{0}, ^k\mathbf{z}_{1:T}^{1:A-1}]\] -
潜在変数を関数\(f_{\theta}(\cdot)\)を使って予測経路に変換する
\[^{1:K}\mathbf{s}_{1:T}^{1:A} \leftarrow f_{\theta}(^{1:K}\mathbf{z}_{1:T}^{1:A}, \phi)\]
どうやって有効だと検証した?
ESPの検証
Didactic Example:シンプルなシミュレーターを作成し、そのシミュレーター上でモデルを訓練し、検証した。作成したシミュレーターはロボット(青)と人間(オレンジ)の2つの車両が互いに違う方向から同じ交差点へ向かう動作をシミュレートする。ロボットと人間はそれぞれ動作を行う。
- ロボットは交差点を直進しようと試みるが人間が左折した場合には譲歩する。
- 人間は常に4ステップ直進し、その後50%の確率で直進もしくは左折のどちらかの行動を行う。
比較手法としてR2P2-MAを用いた。R2P2-MAは単一エージェントの経路を予測するR2P2(link, summary)の予測ヘッドを複数にしたモデルである。R2P2-MAは相互作用を考慮しない。
次に示す図と表が検証結果である。

表のPlanning crashesより、R2P2-MAは50%の確率で人間とロボットがぶつかる予測を行うが、ESPはぶつからない予測を行うことがわかる。この結果はESPは人間の決定に対して反応した経路を予測することを示している。
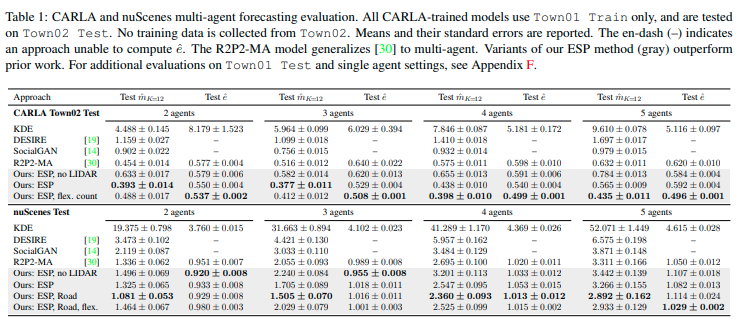
CARLAおよびnuScenes:CALRAおよびnuScenesから10個のデータセットを作成し、モデルの予測性能を検証した。ベースラインとしてKDE、DESIRE、SocialGAN、R2P2-MAを用意した。また提案モデルESPのバリエーションとしてESP, no LIDAR、ESP, Road、ESP, flexを用意した。ESP, no LIDARは観測からLIDARを除いたESP、ESP, RoadはnuScenesの道路領域をバイナリマスクで表現した入力を追加したESP、ESP, flexは可変数のエージェントに対応するESPである。
次に示す表が検証結果である。表よりCALRAおよびnuScenesの両方のデータセットでESPの性能が比較手法の性能を上回っていることが確認できる。
PRECOGの検証
ESPの検証と同様に、CALRAおよびnuScenes上でPRECOGの予測性能を検証した。グランドトゥルースの自動運転車両の最後の時刻における位置をゴールとして設定し、PRECOGで経路を予測した。比較手法としてDESIRE、DESIRE-plan、ESPを用いた。
次に示す図および表が検証結果である。表に示す\(\text{Test} \hat{m}_K\)は自動運転車の予測経路の評価結果である。\(\text{Test} \hat{m}_K^{a=1,2,3,4,5}\)はその他のエージェントの予測経路の評価結果である。自動運転車から距離が近い順に表示されている。

表よりPRECOGの有効性を示す次のことが確認できる。
- PRECOG > ESP > DESIREの順で結果が良い。
- PRECOGの予測結果を見ると自動運転車\(\hat{m}_K^1\)だけでなくその他のエージェントの予測性能が向上している。特に自動運転者に近いほどその向上する割合が大きい。
課題は?議論はある?
さらなる精度向上のため、自動運転車だけでなく他のエージェントにもゴールや事前知識を使って条件付けることが考えられる。
次に読むべき論文は?
Contingencies from Observations: Tractable Contingency Planning with Learned Behavior Models
Deep Imitative Models for Flexible Inference, Planning, and Control
Deep Structured Reactive Planning
補足
使われた仮定及び各変数の詳細
連続空間、離散時間、POMDPのマルチエージェントシステムを扱う。時刻\(t\)におけるすべてのエージェントの状態(位置)を\(\mathbf{S}_t \in \mathbb{R}^{A \times D}\)とする。\(A\)はエージェント個数、\(D=2\)である。変数を関数と区別するためにボールドで表す。大文字は確率変数であることを示す。\(\mathbf{S}_t^a\)は時刻\(t\)におけるエージェント\(a\)の2次元位置\(x,y\)を示す。\(t=0\)は現在時刻、\(a\)が\(r\)もしくは\(1\)の場合は自動運転車両、\(h\)もしくは\(2\sim\)の場合は他車両を示す。添字を省略した\(\mathbf{S}\)は\(\mathbf{S}_{1:T}^{1:A} \in \mathbb{R}^{T \times A \times D}\)を示す。すなわちすべてのエージェントの予測である。\(\chi\)はLIDARや道路などの高次元の観測である。実験した例ではLIDARの情報を俯瞰図で表現した観測\(\chi= \mathbb{R}^{200 \times 200 \times 2}\)を使った。各グリッドの面積は\(0.5 m^2\)であり、地面の上と下にあるポイントの2ビンのヒストグラムである。各エージェントは\(\phi \doteq \{\mathbf{s}_{-\tau:0}, \chi \}\)にアクセスできる。
可変数のエージェントに対応するESP
エージェント数が時刻\(1:T\)の間で変わるようなデータに対して予め最大エージェント数\(A_{train}\)を決めた上でネットワークを設計する。そして予測経路を出力するRNNに欠落しているエージェントを表すマスク\(M \in \{ 0, 1 \} ^{A_{train}}\)を追加で入力する。
個人的メモ
- アーキテクチャ詳細はAppendix Cに紹介されており大きなアーキテクチャの構造の変化はないものの、性能を向上させるための空間特徴量の抽出方法など、いくつかの変更点がある。