matomEmotam

読んだ論文のまとめ

Project maintained by KohMat Hosted on GitHub Pages — Theme by mattgraham

[日本語まとめ] Deep Imitative Models for Flexible Inference, Planning, and Control

Nicholas Rhinehart, Rowan McAllister, Sergey Levine

どんなもの？

この論文は模倣学習とMBRL (Model Based Reinforcement Learning)の両方の利点を持つ方法Deep Imitative Models(DIM)を提案する。DIMはエキスパートの行動の分布を模倣する生成モデルを使い、潜在変数からエージェントの行動のサンプルを生成する。次にそのサンプルをエージェントのゴールの達成度を示す目的関数で評価する。そして目的関数を最小化するような潜在変数の勾配を求め、更新する。この手続きを繰り返すことでゴールを達成するようなつエキスパートらしい行動を計算する。

\[\mathbf{s}^{*} \doteq \underset{\mathbf{s}}{\text{argmax}}\ \underbrace{\log q(\mathbf{s} \mid \phi)}_\textrm{imitation prior} + \underbrace{\log p(\mathcal{G} \mid \mathbf{s}, \phi)}_\textrm{goal likelihood}\]

先行研究と比べてどこがすごい？何を解決したか？

模倣学習はエキスパートの行動を模倣するモデルを訓練するアプローチである。訓練された模倣モデルはテスト時にエキスパートが実行しそうな行動の望ましい最良の推測を行う。しかし、テスト時に任意のゴールを設定し、そのゴールを達成するような行動を選んでモデルを動かすことはできない問題がある。もしくはゴールを設定できても、訓練時に設定しないといけなかったり、直進や右左折など簡単なものに限られる制限がある。

一方でMBRLはダイナミクスモデルを使い、目的を達成するように目的関数を最小化するアプローチである。テスト時に自由にゴールを設定できる。しかし、ゴールを達成する目的関数の設計が難しい問題がある。特に目標の達成よりも望ましい行動の設計に試行錯誤を必要とする。複雑な行動であればあるほどその設計難易度は高くなる。

提案手法DIMは両方の問題を解決しつつ、両方の利点を持つ方法である。特にエキスパートの行動をサンプルできるため、望ましい行動の設計の必要性がなくなる。またDIMが６つのILとMBRL（モデルベース強化学習）の性能を上回ることを実験上で示した。

手法は？

DIM

連続空間、離散時間、POMDPの仮定をおく。時刻\(t\)におけるエージェントの状態（2次元位置）を\(\mathbf{s}_t \in \mathbb{R}^{D}\)とする。また観測を\(\phi\)とする。変数をボールド、実数値を小文字、確率変数を大文字とする。\(\mathbf{s}=\mathbf{s}_{1:T}\)とする。

DIMは訓練済みのエキスパートの行動を模倣する生成モデル\(q(\mathbf{S} \mid \phi)\)を使い、実行時に目標\(\mathcal{G}\)に到達するエキスパートらしい行動\(\mathbf{s}^{*}\)を次の最適化問題を解くことで求める。ただし\(\phi\)はエージェントの観測である。

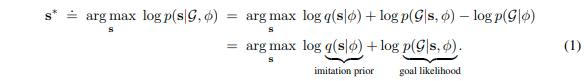
imitaive_planning_to_goals

第１項はエージェントの行動\(\mathbf{s}\)がエキスパートに近いほど高い値となる模倣尤度である。第二項は行動\(\mathbf{s}\)がゴール\(\mathcal{G}\)に近いほど高い値となるゴールの尤度である。

生成モデルは微分可能であるため、上記の最適化問題は次のようにGradient ascentで解くことできる。

imitative_plan

図に示す\(\mathbf{z}\)は生成モデルの潜在変数である。関数\(f(\cdot)\)は観測\(\phi\)と潜在変数\(\mathbf{z}_t\)から行動\(\mathbf{s}\)に変換する可逆かつ微分可能な生成モデルの関数である。

\[\mathbf{Z} \sim q_0; \mathbf{S} = f(\mathbf{Z}; \phi)\]

生成モデル

本論文ではR2P2(summary)を生成モデルとして使う。R2P2は自己回帰型のフローベースの生成モデルであり、LIDARの点群と道路、および潜在変数から自動運転車両の行動\(\mathbf{S}\)を2次元点からなる経路として生成する。具体的には次に示す１ステップ先の更新式を繰り返し使って生成する。

\[\mathbf{S}_{t} = f_{\theta}(\mathbf{Z}_t) = \mu_{\theta}(\mathbf{S}_{1:t-1}, \phi) + \sigma_{\theta}(\mathbf{S}_{1:t-1}, \phi) \cdot \mathbf{Z}_t\]

式中に使われる関数\(\mu_{\theta}(\cdot)\)および\(\sigma_{\theta}(\cdot)\)は状態\(\mathbf{S}_{t}\)の平均および標準偏差を出力するネットワーク関数である。この\(\mu_{\theta}(\cdot)\)および\(\sigma_{\theta}(\cdot)\)の具体的なネットワークアーキテクチャーを次の図に示す。

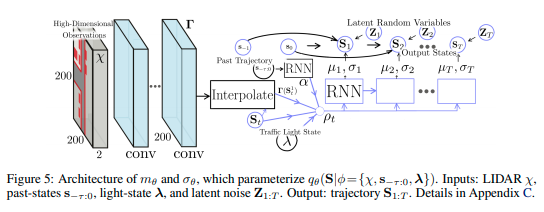
deep_imitative_model

図に示すようにR2P2のネットワークは

を元に次の手順で潜在変数\(\mathbf{z}_{1:T}\)から計画\(\mathbf{s}_{1:T}\)もしくは計画\(\mathbf{s}_{1:T}\)から潜在変数\(\mathbf{z}_{1:T}\)を計算する。

  1. 現在時刻で得られた観測からRNN(GRU)とCNNを使って特徴量\(\alpha\)と特徴マップ\(\Gamma\)を計算する

  2. 時刻1からTまで以下のステップを繰り返す

    1. エージェントの位置\(\mathbf{s}_{t-1}\)に対応した空間特徴量\(\Gamma(\mathbf{s}_{t-1})\)をbilinear補間により特徴マップ\(\Gamma\)から取り出す

    2. 各特徴量\(\alpha\)、\(\mathbf{s}_t\)、\(\Gamma(\mathbf{s}_{t-1})\)および\(\lambda\)はConcatenationして特徴\(p_{t-1}\)を作成する

    3. 特徴\(p_{t-1}\)から予測用のRNN(GRU)を使い、ベレの方法(wiki)のステップ\(m_{\theta}\)と位置の標準偏差\(\sigma_{\theta}\)を計算する

    4. ベレの方法から位置の平均を計算する

      \[\mu_{\theta}(\mathbf{s}_{1:t-1}, \phi) = 2 \mathbf{s}_{t-1} - \mathbf{s}_{t-2} + m_{\theta}(\mathbf{s}_{1:t-1}, \phi)\]

    5. 潜在変数\(\mathbf{z}_t\)から状態\(\mathbf{s}_{t}\)を計算する。もしくは訓練時は状態\(\mathbf{s}_{t}\)から潜在変数\(\mathbf{z}_t\)を計算する

      \[\mathbf{s}_{t} = \mu_{\theta}(\mathbf{s}_{1:t-1}, \phi) + \sigma_{\theta}(\mathbf{s}_{1:t-1}, \phi) \cdot \mathbf{z}_t\] \[\mathbf{z}_t = \sigma_{\theta}(\mathbf{s}_{1:t-1}, \phi) ^{-1} (\mathbf{s}_{t} - \mu_{\theta}(\mathbf{s}_{1:t-1}, \phi))\]

ゴール尤度

ディラックのデルタを使った尤度関数をゴール尤度関数として用いる。

\[p(\mathcal{G} \mid \mathbf{s}, \phi) \leftarrow \delta_{\mathbf{s}_T} (\mathbb{G}),\ \delta_{\mathbf{s}_T} = 1 \text{ if } \mathbf{s}_T \in \mathbb{G}, \ \delta_{\mathbf{s}_T} = 0 \text{ if } \mathbf{s}_T \notin \mathbb{G}\]

\(\mathbb{G}\)はエージェントが達成するべき最終状態のセットである。自動運転の場合、目的の道路を示すwaypointsやline segment、もしくは走行可能領域を\(\mathbb{G}\)とすることができる。

ゴール尤度は以上の設計に限らず、通常のMBRLのように自由に設計することができる。例えば上式で使われたディラックのデルタ分布の代わりにガウシアン関数を使うこともできる。この場合、目標は必ず達成しなければならないものから奨励するべきものになる。他には次の2つの論文で提案されたエネルギーベースの尤度を使うこともできる。

\[p(\mathcal{G} \mid \mathbf{s}, \phi) \propto \prod_{t=1}^{T} e^{-c(\mathbf{s} \mid \phi)}\]

どうやって有効だと検証した？

DIMを自動運転システムに適用し、CARLA上で性能を検証した。特に次の点について調べた。

  1. 最低限の報酬関数の設計とオフライン学習によって解釈可能なエキスパートのような計画を生成できるか？この手法が有効であるか？
  2. 実際の車両の設定のもとでstate-of-the-artの性能を達成できるか？
  3. 新しいタスクに対してどれだけ柔軟であるか？
  4. ゴール設定へのロバスト性はどれだけあるか？

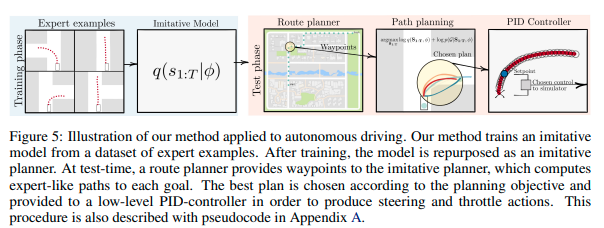
PathPlanning

検証1 走行性能

CALRA上でDIMを動かし、走行性能を他の手法と比較することでDIMの有効性を調べた。比較手法はCIRL, CAL, MT, CILなど以前提案された模倣学習を使った方法およびMBRLによる方法である。またDIMのバリエーションとしてゴール尤度関数を変えたDIMの走行性能を評価した。次に示す表が検証結果である。

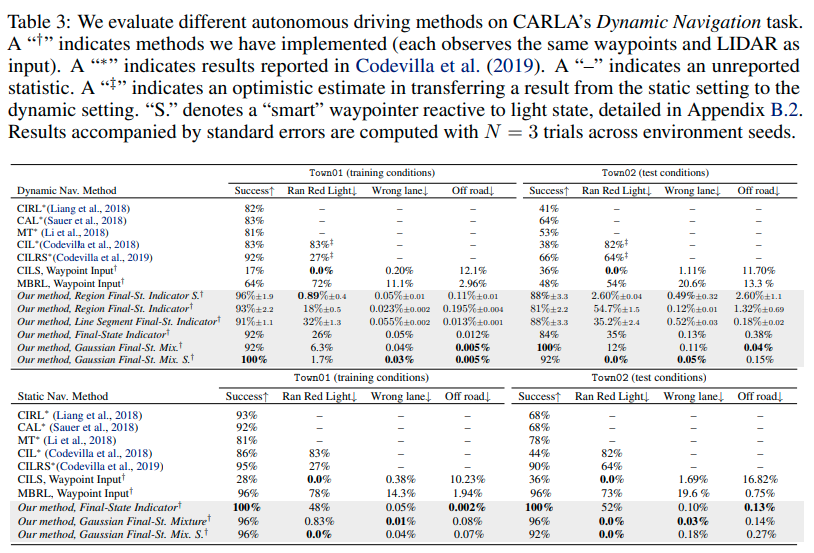
start_of_art_result

表に示すとおりStaticおよびDynamicな環境の両方でDIMが比較手法の性能を上回った。この結果は検証内容1,2に対して肯定的な回答(affirmative answers)を得られたことを示している。

検証2 ゴールノイズに対するロバスト性

検証１の環境に加えてゴールにノイズを加えてDIMを実行し、性能を評価した。ゴールに加えるノイズとして次の２種類のノイズを用いた。

  1. waypointsからなるゴールの半分を、大きく変動
  2. ゴールを自動運転車両がいる車線の対向車線に設定

以上のいずれの場合も高い確率でナビゲーションを成功させることができた。この結果は検証内容４に対して肯定的な回答を得られたことを示している。

検証3 potholeの回避

検証１の環境に加えて自動運転車両が走行する道路上にランダムにPotholeを追加して、DIMが追加したPotholeを回避できるかどうかを検証した。検証に当たってGaussian Final-State MixtureおよびEnergy-based likelihoodを組み合わせたゴール尤度を使用した。次の図に示すようにDIMはセンターラインに近づいたり、時には反対レーンに行くなどしてPotholeを避けるナビゲーションを行うことができた。

goalsettings

検証4 経路計画の信頼度推定

生成モデルが計画を安全でない計画を正しく判断できるかの実験を行った。エキスパートが実際に行った良好なwaypointと道路外にある悪いwaypointが含まれる1650のテストケースに対してリコール97.5％、精度90.2%を示した。

またあるウェイポイントが計算した計画の信頼区間に含まれる確率を計測した。信頼区間は、計画の基準の平均値から1標準偏差を引いた値を計画の基準の閾値とした区間である。

  1. エキスパートが時間Tに実際に到着したウェイポイントは89.4%
  2. 提供されたルートに沿って20m進んだ先のウェイポイントは73.8%
  3. 2)のウェイポイントから2.5mずれたウェイポイントは2.5%

この結果から有効なウェイポイントを正しく判定する傾向があることがわかる。

検証5(課題) 信号のノイズに対するロバスト性

DIMが観測する信号の状態にノイズを加えてCARLA上でナビゲーションを行った。20％の確率で緑を赤、赤を緑として観測する。実験結果を次の表に示す。

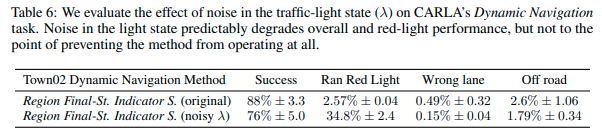
traffic_light_noise

表より概ね成功しているものの、赤信号に対してより違反を行うという傾向があることが確認できる。また交差点付近で停止と発進を繰り返し行う挙動が見られた。ノイズを加えた状態で訓練することによりよりロバストになる可能性がある。

課題は？議論はある？

ゴールノイズに対する実験でノイズとして入れたwaypointが交差点内の有効な場所ではあるが、目的地へ向かう方向ではない場所に設定されたときに、プランナが一時的に最適なルートを生成できないことがある。

観測のノイズおよび分布外の観測に対するロバスト性に対していくつかの課題がある。

  1. 提案モデルは現時刻の観測のみを元に将来の行動を予測している。よりロバストにするためにはベイジアンフィルタリングを使うことが考えられる。しかし、高次元のフィルタリングは多くの場合手に負えないので、ディープラーニングをつかった近似ベイジアンフィルタリングを行う必要がある。
  2. 訓練データ分布外の観測に関するロバスト性を向上させるため、Deep Ensemble Networkを使う方法が考えられる。

Balaji Lakshminarayanan, Alexander Pritzel, and Charles Blundell. Simple and scalable predictive uncertainty estimation using deep ensembles. In Neural Information Processing Systems (NeurIPS), pp. 6402–6413, 2017.

次に読むべき論文は？

A. Filos, P. Tigas, R. McAllister, N. Rhinehart, S. Levine, and Y. Gal, “Can autonomous vehicles identify, recover from, and adapt to distribution shifts?” arXiv preprint arXiv:2006.14911, 2020.

N. Rhinehart, R. McAllister, K. Kitani, and S. Levine, “PRECOG: prediction conditioned on goals in visual multi-agent settings,” in Proceedings of the IEEE International Conference on Computer Vision, 2019, pp. 2821–2830.

個人的メモ